Abstract algebra (the study of groups, rings, fields) and differential geometry are my favorite courses in undergraduate study. I enjoyed a lot studying the very elegant and imaginative two subjects of mathematics back then. Unfortunately, my master's study in computer vision has little to do with them (now there is more!): after 5 years of engineer path, many terms became vague.

There could be countless reasons I just keep letting these knowledge go vanishing in my memory, until recently I came across very exciting research in machine learning that heavily utilities group (representation) theory and differential geometry. During reading it I had this estranged excitement: I am over the moon to see the familiar terms in pure mathematics appear in state of art ML research, but sadly I can't totally understand every detail of those papers. So I decided to write a series of posts, from the very basics of group theory / differential geometry, until a mature understanding of the recent research on convolution neural networks on Riemannian manifold, mainly to do myself a favour 😼

Groups

For mathematicians, group is a very basic concept which appears every where: integers under addition forms a group; all roots of a polynomial equation forms a group; vector space is a group with extra structure; every possible move on a Rubik's Cube forms the Rubik's Cube group; a periodic wallpaper pattern gives rise to a wallpaper group...

And for the rest of us, people either never heard of it, or know it by name but has weird imagination in mind about it (I once heard in a podcast where people confused it with categorical theory and comfortably referred this term for half an hour). So let's start from the basics.

Group is not so well-known as matrix, but it also plays a fundamental role in mathematics, especially when it has something to do with symmetry, which we will explore later. With the help of group theory (specifically, Galois theory), the ancient geometric problems such that the impossibility of doubling the cube and Angle trisection are proved. In algebra, another famous example of Galois theory's power is to prove the impossibility to get a general solution of quintics.

To form a group, we need a set $G$ (e.g. the set of all integers) and a binary operation $\cdot$ on the set, which combines any two elements $a$, $b$ in the set, the result $a \cdot b$ still belongs to $G$. Additionally, to make $(G, \cdot)$ a group, three axioms must be fulfilled:

• Associativity: $\forall a, b, c \in G$, $(a \cdot b) \cdot c = a \cdot (b \cdot c)$

• Identity element: $\exists e \in G$, such that $e \cdot a = a \cdot e = a$

• Inverse element: for $\forall a \in G, \exists b \in G$, such that $b \cdot a = a \cdot b = e$, we denote $b = a^{-1}$

It's not hard to prove that the identity/unit element, and inverse element of any member of a group is unique.

Before we dive into more example of groups, it's good to know the concept of a Albelian Group, or Commutative Group, which means simply for any $a, b \in G$, we have $b \cdot a = a \cdot b$.

Examples 🐯 📖 🍋 🌵

• $(\Z, +)$: integer group with addition operation: the associativity of addition of numbers is trivial in this case; $0$ is the identity element and the negative of each number plays the role of inverse element of integer addition group.

Till here, it seems group theory justs add some rigid terms to something we already know from primary school, but the more example / counter examples you learn, you will see the beauty of describe the numbers or operations we know as well defined algebra structure.

To serve as a counter example, can you tell why $(\Z, \cdot)$, i.e. integers with multiplication as operation, is not a group?

• $(\mathbb{Q}^{*}, \cdot)$: the set of all non-zero rational numbers with operation of multiplication forms a group, with $1$ as identity element and the reciprocal serves as inverse element.

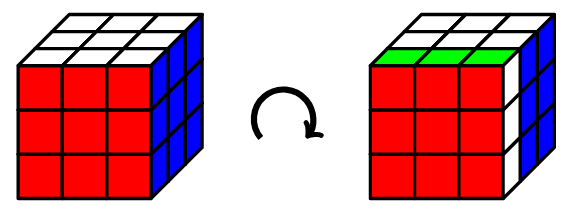
• Rubik's cube group: the set $G$ corresponds to all legal positions of a Rubik's cube, and the operation $\cdot$ is the composition of cube moves (a cube move is the rotation of a particular face in the clock-wise direction by 90 degrees, so there are in total 6 of them). The identity element is the solved Rubik’s Cube, which corresponds to the empty sequence of cube moves. Furthermore, we expect that any legal position has an inverse, since we know even a $3 \times 3$ cube has over 43 quintillion legal positions, any position can be solved in 20 or fewer moves.

Different from $(\Z, +)$ and $(\mathbb{Q}^{*}, \cdot)$, Rubik's cube group is non-albelian, because two different moves on a cube are not commutative. Rubik's cube group might not be most mathematically interesting, but it serves as a nice illustration of permutation group.

Matrix groups

With an minimalist impression of groups in mind, we can dive into a class of (engineer-wise) very useful groups which consist of matrices together with matrix multiplication as operation.

• $GL(n, \mathbb{R})$, General Linear Group: consists of all invertible n-by-n matrices with real entries. The existence of matrix inversion and identity matrix fulfills the group axioms.

• $GL^{+}(n, \mathbb{R})$: a subgroup of $GL(n, \mathbb{R})$, contains matrices with positive determinant. $GL^{+}(n, \mathbb{R})$ represents all the orientation preserving linear transformations of $\mathbb{R}^{n}$ (keeps the left-handed and right-handed orientation).

• $SL(n, \mathbb{R})$, Special Linear Group: is a subgroup of $GL(n, \mathbb{R})$, whose element has determinant 1. special linear group can be characterized as group of volume and orientation preserving linear transformations of $\mathbb{R}^{n}$.

• $O(n, \mathbb{R})$, Orthogonal Group: is the group of orthogonal matrices, it is a subgroup $GL(n, \mathbb{R})$, represents the group of distance preserving transformations of a Euclidean space of dimension $n$.

• $SO(n, \mathbb{R})$, Special Orthogonal Group: contains orthogonal matrices of determinant 1. It preserves orientation, angles and distance. It is also called rotation group, in the case of $n=3$, noted as $SO(3)$, it describes all rotations about the origin of 3D Euclidean space. For example, in computer vision, all camera rotations belong to $SO(3)$.